Local license key verification - Theory
If you’ve ever entered a license key for software activation you might’ve experienced the software verify the validity of the key without the need for internet connection. The most popular example would be a Windows installation, during that time your computer most likely does not have the necessary drivers to be connected to the internet. This was for sure more true in the era of Windows XP, but the installation still has the ability to accept a key without an Ethernet cable plugged in to this day.
Imagine that you are developing a small application and you want to share it with others but you still want to license it and don’t want to share it for free. You don’t want to go out full guns blazing and create a server for online verification, you’re thinking about doing it completely local. Goals are to allow you to quickly generate a new valid license, verify it and maybe ban some licenses if they ever become shared too much on the internet. If you want to have a fun challenge, try to come up with some solution to this problem under these contrasts. For people that don’t have the energy or motivation to think I’m going to move on and talk about some possible solutions.
Goals
Firstly I’m going to define some aspects that need to be considered in each solution:
- Simplicity: is it simple to implement and add to your code base
- Security: can a keygen be created for that algorithm
- Extensibility: can you store some additional information in the key itself
- Human friendliness: can the key be short enough to be typed by hand
Solution 1: Parity or other checksums
According to this Stackoverflow answer, Half-Life and StarCraft had 13 digit long license keys, the verification step treated the first 12 digits as the payload and the last digit as the checksum. This approach is really simple, you generate some gibberish and later using those random bytes produce a hash or a checksum and append that to the key. The simpler the checksum generation algorithm the easier it is to code it from scratch. But since the same algorithm that was used during generation has to be present in the binary for verification it’s possible for some malicious actor to reverse engineer (RE) that algorithm. With the algorithm in hand a program can be created that will generate new random bytes and run it through the same checksum algorithm thus creating a new, completely valid key. Such a program would be called a keygen. If you think that being clever and creating a complex checksum algorithm is going to stop people I suggest taking a peek into pirated software land and notice the amount of keygens still available. The first bytes do not need to be random, you can actually store some information in there like the product ID number, type of license, or some variables that will control the availability of given features. If you make the payload small, the overhead is minimal since we would only need something like 4 bytes at most to checksum the data. This solution is not sophisticated, but accepting any input is still worse, think of it as having a fence around your castle, it’s not going to protect it against people that really want to get in but it will deter most of the passerby’s. What is really happening is that we are exposing our internal data to everyone, and if someone knows what we expect he can provide that information, we would need to somehow encrypt the data that we keep in the key.
Possible implementation might use a Cyclic Redundancy Check (CRC), you might’ve heard about this from fields where transformation and or storing of the data is important.
A one sentence explanation of what CRCs are is that they are n-byte - where n is most commonly a power of 2 between 1 and 8 - remainder of polynomial division when the message is treated as a big polynomial that is going to be divided and a divisor that is hard-coded.
I’m really not going to try to beat Ben Eater’s “How do CRCs work?” video, if you want to understand that from the ground up i really recommend it.
If you want for simplicity’s sake, think of CRCs as a hash, but be wary that they really are not the same, hashes and checksums have different goals in mind and using a checksum where a hash should be used or vice-versa could be disastrous.
For the rest of the paragraph is assume that the reader is knowledgable in the ways that CRCs work.
It’s simple enough to implement a CRC calculating function from scratch, I’ve based my code on Hacker’s Delight from figure 14.6.
I’m not using the standard CRC32, by that I mean different generator, no reversing of incoming or outgoing bits and no xor of the result.
After looking into the Philip Koopman’s generator polynomial tables I’ve chosen the 32 bit in size and 8 Hamming Distance, so G is 0xf8c9140a.
If you choose to implement your own CRC function from scratch you can check if you produce the right result with this calculator or this one if your generator is not on the list of supported CRCs.
Here is my code that aims to be simpler rather than fast, it look like it belongs on r/programmerhorror but if you study it and really come into the mind set of a CPU it’s actually just the software version of the diagram 14.3 from Hacker’s Delight.
u32 CRC32KoopmanHD8(const u8 *bytes, u64 count) {
u32 g = 0xf8c9140a;
u32 crc = 0;
for(u64 i = 0; i < count; i++) {
crc ^= (((u32)bytes[0]) << 24);
for(int i = 0; i < 8; i++) {
u32 mask = -((crc & 0x80000000) >> 31);
crc = (crc << 1) ^ (g & mask);
}
bytes++;
}
return crc;
}
Solution 2: Symmetric key cryptography
Since I mentioned Windows XP in the beginning how does it verify keys? We are in luck because in this paper the algorithm is explained in great detail and it’s full of fun things that the verifier does in order to be human friendly. At the core the verification comes down to key containing 17 bytes of useful information, 16 of those are encrypted using a Feistel cipher, if you don’t know what that is, pretend I said AES-128 - it’s not the same but I want to get the idea across. If I’ve peaked your interest I highly suggest reading that paper, has some good stuff in there. Back to the topic at hand, how can be build something on top of that? It’s up to us really, we can increase the security of our checksum key approach from the previous solution by encrypting the whole key and instead of digits make the key be base64 or some other system of writing arbitrary bytes values as human readable text. In the verification step, we are going to decrypt the bytes and check the checksum. This approach is bit more complicated because we need to support some kind of symmetric encryption, but many CPUs support AES256 as intrinsics so the implementation might be really simple. Since the encrypting and decrypting key is the same and it needs to be stored in the binary it’s still possible to create a keygen for your software. At the first glance the security really improved, and the key looks more like random noise than a structured thing that might be RE by just looking at the raw bytes. Now our verification won’t be broken in a afternoon as a challenge for someone learning Ghidra but it might be a part of a three day course on creating keygens.
Solution 3: Merkle trees
Since you need to understand what Merkle trees are in order to understand how this approach would work I’ll try to provide a simple explanation.
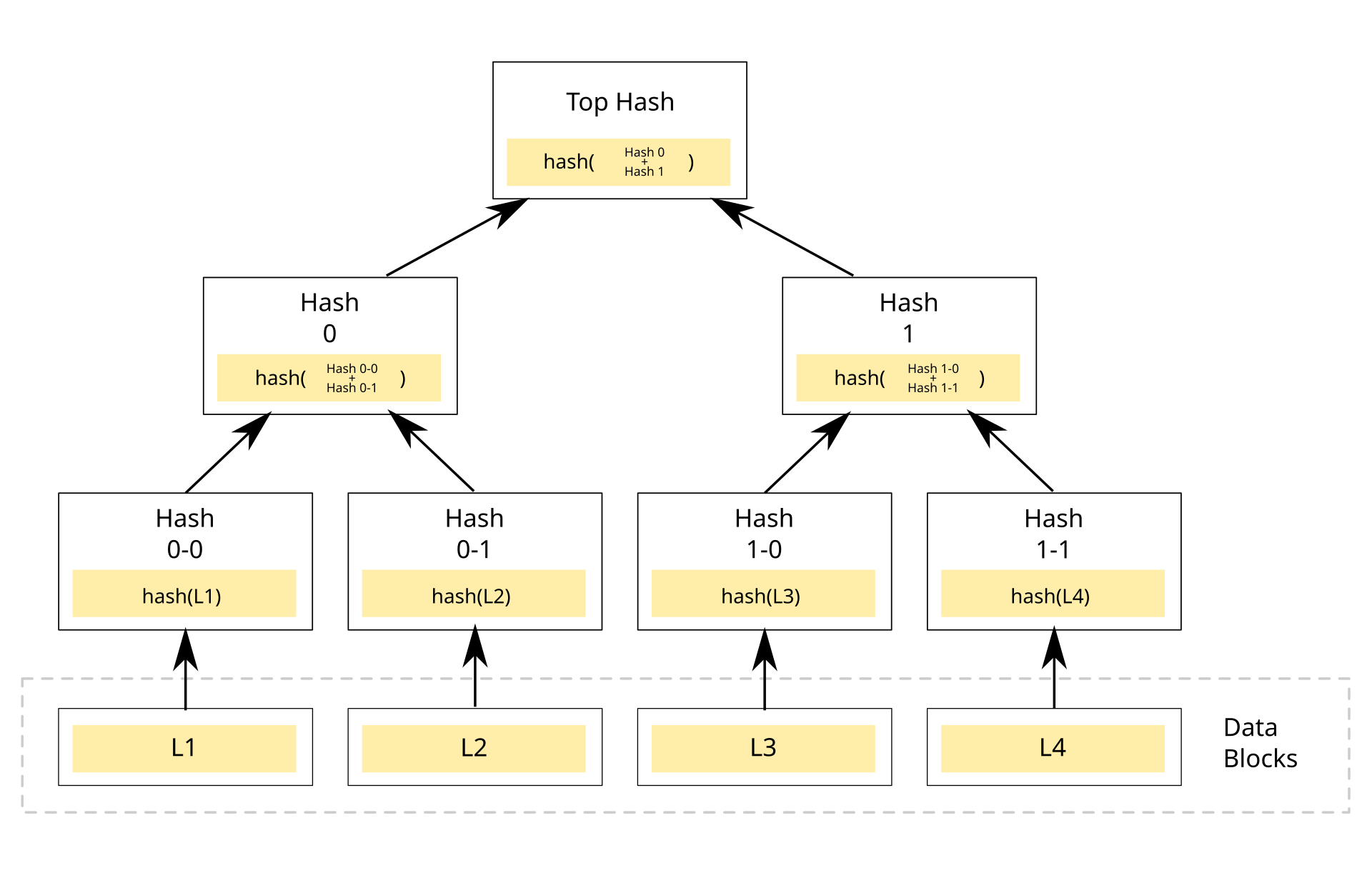Imagine that you have an array of some items, in the image above depicted as L1..L4.
How can you prove that some element L is contained in the array without the need to expose the entire array to the verifier?
If you compute a hash of each element in the array you have the hash of each leaf, now to compute a hash of each parent node we are going to concatenate the hash of the left leaf with the hash of the right leaf and compute a hash of that, do that recursively up to the root.
Now the verifier needs to store only the root hash to verify that an element is part of the tree.
Let’s suppose that we want to verify that the element L3 is part of this tree, we would need to provide the following information to the verifier: L3, hash(L4) and hash(hash(L1) + hash(L2)), in the imaged labeled as “Hash 0”.
That’s the entire information we need to compute the root as the verifier, if the computed hash is equal to the stored root hash then that element is part of the array.
The entire concept is based on the fact that it’s impossible to determine what input L produced a hash(L).
How can we build a licensing scheme using that data structure?
If we can guarantee that we will not need more than n license keys, we can pre-generate the keys ourselves and build a tree out of them.
Now while compiling the application we only export the following information in the binary: root hash and the hashing algorithm.
The key in this scheme would be an element from the data array and all needed intermediate hashes.
This solution is the first approach that is completely secure against keygen’s, since in order to create a valid license key a malicious actor would need to know all the keys that we’ve pre-generated.
That’s the only pro of this solution, the cons on the other hand are more numerous.
Firstly, the number of licenses is limited, we could of course create a new tree and add it to the new release of our software but it seems a bit hackish.
Lastly, the number of bytes needed to represent the information is much bigger then before.
You can see how the amount of hashes needed to be encoded in the key are log2(n) where n is the number of pre-generated license keys.
If MD5 is chosen for the hash function it’s output size is 128 bit, so to store the entire tree we would need 320 bytes if we chose to generate 1 million keys.
We can of course choose to cut the output to 32 or even 16 bits, which would require only 80 or 40 bytes, but this is starting to be to big to comfortably typed by a human from a piece of paper.
This is as simple to implement in your code as simple you chose your hash function, but pretty please, do not choose the MD5 hash function since it’s security is spotty at best.
Solution 4: Asymmetric key cryptography
Now this solution is has almost all of the best parts from the previous solutions, this approach is considered modern, for example by keygen.sh. Most of the time public keys are used for encryption and private keys are used for decryption, even Wikipedia begins with saying that “anyone with a public key can encrypt a message”. If you look two paragraphs down they say something about signing, which is the reverse role of the keys. By that I mean that the private key is used to encrypt the data and public key is used for decryption. Since the public key is as the name suggests widely known, why would we want to decrypt with it? Well, because we can confirm that whoever encrypted this message has to know the private key tied to this public key we can confirm authority. This logic is at the basis of certificates in the internet, for example Google does not share it’s private key, it uses it only to encrypt some message. Any body with the public key can decrypt that message and confirm the only Google could’ve encrypted this message so we can trust this data. In the license key scenario, in the binary file we store only the public key and keep the private key a secret. We are going to encrypt the data we want to use for confirming the key itself with the private key and in the program we only need to decrypt the data and see if it’s valid. Security of the checksum solution combined with this approach is promoted from a fence around the castle to a whole lava pit and archers with their bows drawn. Since the resulting encrypted data size is tied to the bit size of the key - more precisely the modulus in RSA - with a 1:1 relation, the encrypted license key would need a lot more bytes then previous solutions. For the smallest key size considered to be safe in today’s world which is 2048-bit, the encrypted license key size would be 256 bytes, which after base64 encoding is going to need ~342 characters. This is untypeable by a real person, so printing something like this on a CD box is beyond stupid but sending something like this over e-mail or any other medium where someone can just copy-paste the key is still a valid option. Saying that, keep in mind that Elliptic Curve Cryptography (EDC) can achieve the same strength of encryption that a 3072-bit RSA key with using only 256-bits. Using for singing the license key size would be 32 bytes or encoded in base64 ~43 characters, someone could type that by hand but it’s still better to assume that they are going to be copying in that from an e-mail.